Better Idea: Computational Graphs
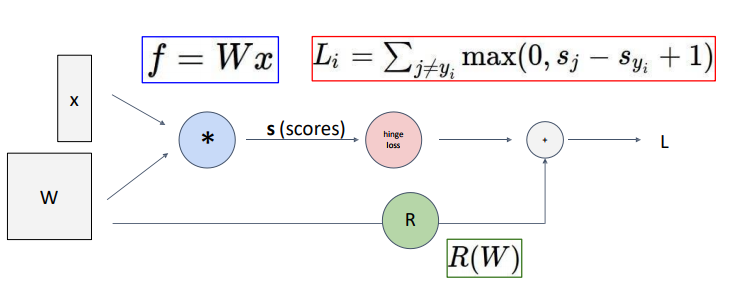
복잡한 함수의 Analytic gradient을 쉽게 계산하기 위해서 computation graph을 그린다.

sigmoid function을 통해 좀더 간편하고 효율적으로 gradient를 계산하는 것을 보여준다.
이와같이 computational graph의 최종 loss를 통해 input단의 original parameter들의 gradient를 계산하는 backpropagation과정에서 나타나는 몇개의 pattern을 볼 수 있다.
Patterns in Gradient Flow

- add function(add gate) : gradient distributor 역할
- mul function(mul gate): swap multiplier 역할
- copy function(copy gate) : gradient adder 역할
- max function (max gate): gradient router 역할
So far: backprop with scalars
What about vector-valued functions?
그런데, 차원이 변할 수 있다.어떻게 이 과정을 거칠것인가?
Recap: Vector Derivatives

- Input, output이 모두 scala일때는, 미분도 scala로 정의가 된다.
- output은 scala, input은 vector인 경우, gradient는 input과 차원수가 같다. gradient의 n번째 component는 n번째 input이 조금 변화했을 때, 전체 output이 얼마나 변하는 지에 대한 값이다.
- Input, output이 모두 다변수인 경우에, 미분(derivative)은 jacobian으로 표현된다. jacobian의 (n,m) component는 n번째 input이 변화할 때, m번째 output의 변화 정도를 의미한다. 훨씬 간단하고 효율적으로 표현하고 계산된다.
Backprop with Vectors

여기서 input은 각각 x, y 두 벡터이고 (Dx, Dy로 표기) output은 역시 vector인 z이다. (Dz로 표기)
- 여기서 z가 vector라고 해서, loss가 vector 형태일 거라고 생각해선 안된다.
- 최종 loss값은 항상 scalar다.
따라서 upstream gradient인 dL/dz의 의미?
이 node의 output인 z의 각 원소들이 아주 미세하게 변할 때, scalar값인 loss가 어떻게 변하는 지를 의미한다.
좀 더 수학적으로 말하면 dL/dz 벡터는 loss값을 z로 편미분한 벡터다.
dz/dx 의 의미는 이 node에서 함수 f에 대해 입력 벡터 x의 각 원소들이 미세하게 변할 때
출력 벡터 z의 각 원소들이 얼마나 변하는 지를 편미분한 local gradient이다.
그런데 함수 f는 여러 개의 변수 (여기서는 x, y)를 가진 다변수 벡터함수(vector valued function) 이다.
* 여기서 벡터함수는 벡터를 입력 받아 벡터를 출력하는 함수를 의미하는 함수로 쓰였다.


- max gate의 backprob시 upstream gradient가 양수인 값만 1으로 표현된다.
- Jacobian 행렬이 sparse하며 off-diagonal 값이 모두 0이므로 explicit한 방법 대신 implicit multiplication을 수행한다.
Backprop with Matrices (or Tensors)

tensor란 vector와 matrix를 일반화한 것을 뜻한다.
위의 그림의 경우 입력값 x, y와 출력값 z는 matrix 형태다.
upstream gradient는 y와 r같은 형태의 행렬로 주어진다.
여기서 자코비언 행렬은 [(Dx * Mx) * (Dz * Mz)] 처럼 very high rank tensor가 된다.
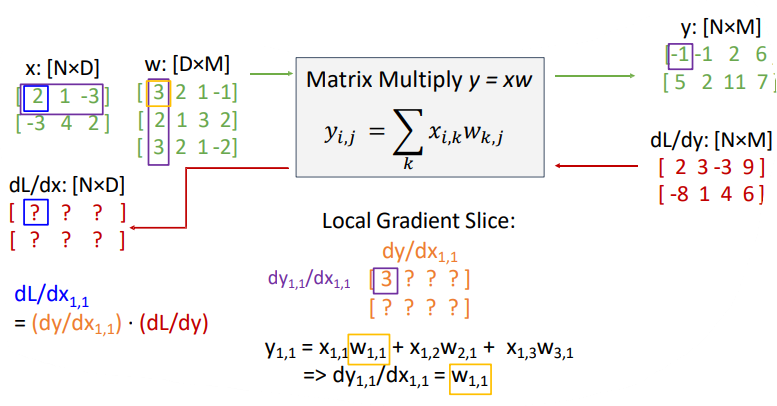
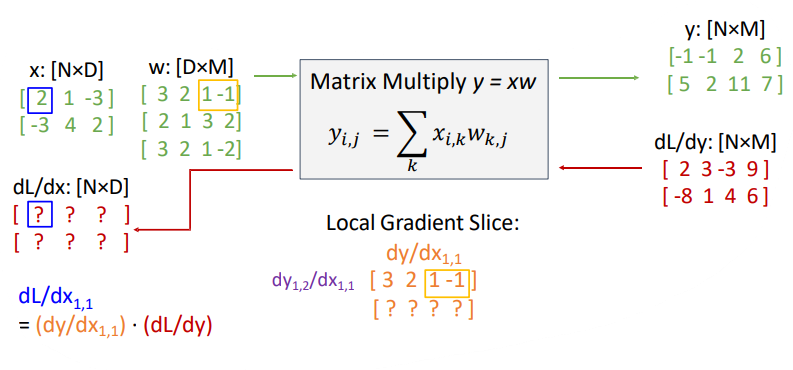
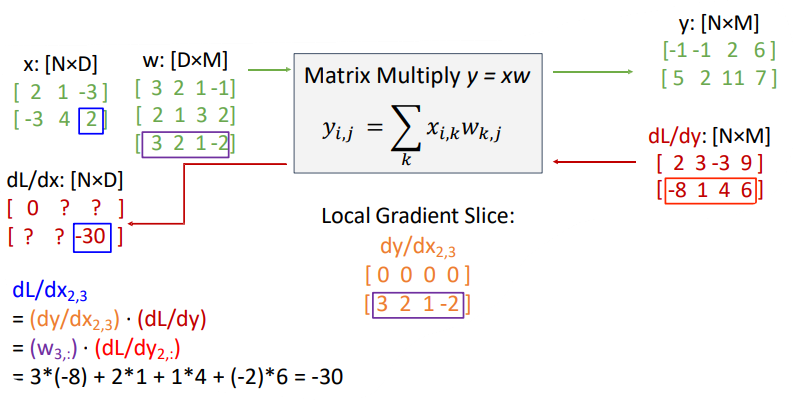
Example: Matrix Multiplication












'Lecture > 딥러닝' 카테고리의 다른 글
| [Dropbox] 코랩에서 Dropbox 사용해서 사진 불러오기 (0) | 2023.07.14 |
|---|---|
| [딥러닝] CNN Architectures (0) | 2023.05.18 |
| [딥러닝] Evaluation Metrics & Training Neural Networks, Part I (0) | 2023.05.18 |
| [딥러닝] Convolutional Neural Network(CNN) (0) | 2023.05.18 |
| [딥러닝] Backpropagation, Optimization (0) | 2023.05.18 |




댓글