지난시간까지 loss를 정의를 했다.
Optimizaion
손실 함수 값을 최소화하는 파라미터 값이다.
최적화 된 w를 찾아서 예측하려는 것이다.
기울기를 따라서 w를 최적화하는 방법이다. 즉 optimization은 산속에서 눈을 가리고 최저점을 향해 헤매는 과정이라 보면 된다. w를 찾아 나가는 것이 loss, 즉 기울기가 줄어드는 곳이다.
많은 경우에 랜덤하게 정한다.
Gradient Descent

최적화 방법 중 하나로 손실 함수의 크기를 최소화시키는 파라미터이다.
학습 데이터 입력을 변경할 수 없기 때문에, 손실 함수 값의 변화에 따라 가중치(weight) 혹은 편향(bias)을 업데이트해야 한다.
Stochastic Gradient Descent(SGD)

현실적으로 많이 사용하는 방법은 mini-batch이다.
training set에서 일부만을 사용해서 보다 속도와 효율성을 높이는 방법의 최적화이다.
일부만을 활용해서 gradient를 계산하고, 이를 통해 parameter를 업데이트 하는 것이다.
Q. How to compute gradients?
가장 간단한 방법은 Backpropagtion

Computational Graph
Deep Network(AlexNet)

많은 도함수가 있다. 이건 AlexNet이라는 Convolutional network를 computational graph로 나타낸 것.
-> 뒤에서 자세히!
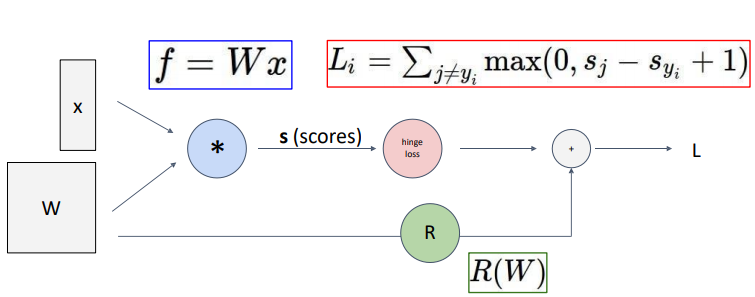
Backpropagation : a simple example

q가 forward pass, f가 backward pass이다.
우리가 원하는 것은 각각의 gradient이다.
왜냐면, 입력값이 x, y, z일 때, 이 x, y, z값이 마지막 output 값에 끼치는 영향을 알고 싶은데, 그것이 바로 저 편미분 값이기 때문!

차근차근 <-방향으로 값을 구해보자.
- f를 f로 미분하면 1
- f를 z로 미분하면 f=qz이므로 편미분하면 q, 즉 3
- f를 q로 미분하면 z값인 -4
- f를 y로 미분하면 연쇄법칙을 해야한다. 즉 f를 q로 편미분한 값과 q를 y로 편미분한 값을 곱하면 -4*1 = -4
- f를 x로 미분하면 연쇄법칙을 써야한다. 즉 -4*1 =-4

FP : 입력값을 받아서 loss값을 구하기까지 계산해 가는 과정
- 우선, x값과 y값을 입력으로 받고, f라는 함수에다가 집어넣어서 z라는 값을 얻어낸다.
- 이때, 우리는 z를 x로 미분한 값과, z를 y로 미분한 값들을 얻어낼 수 있다.
그러고, z를 끝으로 L, 즉 loss를 계산했다고 해보자.
BP : forward pass가 끝난 이후 역으로 미분해가며 기울기 값들을 구해가는 과정
- 마지막에서 시작한다. 즉, L을 z로 미분한다.
- L를 각각 x, y로 미분한 값을 구할 때면, 아까 구해놨던 z를 x,y로 미분한 값과 chain rule을 사용하여 구할 수 있다.
- 그리고, 이 값들을 구한다.
Backpropagation : another example


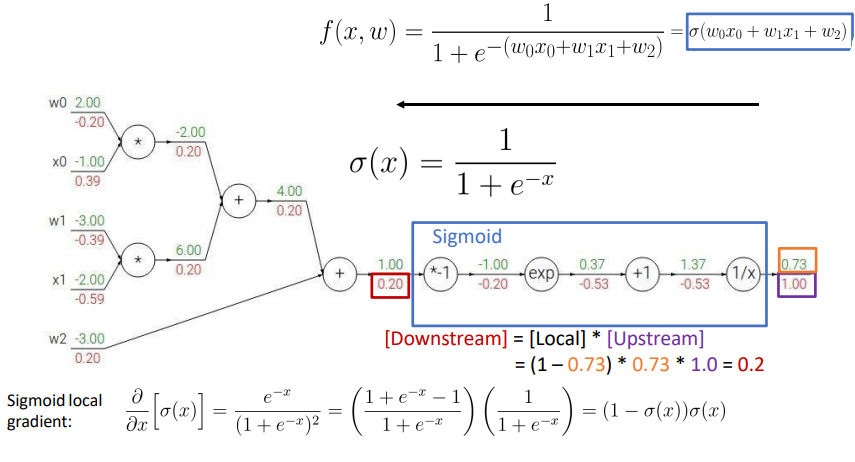
여기서, 어떤 것을 미분하려고 할 때, sigmoid라고 적혀있는 저 부분만 떼서 보았을 때, 저 부분을 한 번에 미분이 가능하다.
묶어서 보면, up이 1이고 local은 1
즉, 0.73 부분에서 1/x부분 미분해서 -0.53, +1 미분해서 -0.53... 할 필요 없이,
그냥 한 번에 (0.73)*(1-0.73) = 0.2 라고 계산이 가능하다는 것이다.
안에 있는 것이 아니라, dl/dx를 바로 구할 수 있다는 것이다.
띠용?? 그럼 지금까지 했던 모든 미분을 죄다 한번에 할 수도 있는 거 아님?? 할 수도 있는데,
사실 맞음! 엄청나게 긴 computational graph조차도 한방에 미분이 되게 할 수도 있다.
그런데.. 위에서 봤다시피 엄청나게 복잡하고, 수없이 많은 노드들이 연결되어 있는 그래프 같은 경우에는, 이게 사실상 불가능하겠죠?
그러니깐, 위의 sigmoid function과 같이 자주 사용되는 임의의 부분만 떼와서, 그 부분만 쉽게 계산할 수 있도록 하면 됩니다.
그런데 sigmoid function이 뭐냐고요??
그냥 중간에 껴들어가는 함수 언저리다~! 하고 생각하시면 됩니다. 나중에 다시 나오니깐, 뭔지 모르겠다고 끙끙대지는 마세요!
그래서 이런식으로 하면 모든지간에 이런식으로 계속 update해나가는 것이다.
Optimization (more than SGD)

다시 위의 것 복습!
일반 Gradient Desent를 다른 말로 batch라고 한다. 모든 값을 한번에 하니까 !
근데 데이터가 많으면 SGD를 한다. 이것은 일부분만 하는 것이다.
minibatch라고도 한다. 이 때는 2의 배수(32,64,128)으로 사용하기도 한다.
Gradient Descent

그럼 실제로 계속 업데이트를 해나갈텐데 이것이 gradient가 되고, w바뀌고, 또 하고.... 계속 반복해서 나가는게 학습되는 과정이다.
이 최적화 과정은 기본적으로 손실함수를 차근차근 줄이는 방향으로 내려가는 Gradient Descent 알고리즘으로 정의된다. 현재 가진 weight 세팅(내 자리)에서 내가 가진 데이터를 다 넣으면 전체 에러가 계산이 되고, 거기서 미분하면 에러를 줄이는 방향을 알 수 있다는 것이다. 그래서 에러를 낮추는 방향으로 가중치를 변경해야 되기 때문에 negative한, 즉 음수 방향으로 정해진 learning rate를 곱해서 weight를 이동시키게 된다.
즉, Weight의 업데이트 = Loss 줄이는 방향(descent) * 보폭(learning rae) * 현 시점의 기울기(gradient)
학습 하기 전에 꼭 정해야 하는 것들!
Hyperparameters:
- Weight initialization method
- Number of steps
- Learning rate
Stochastic Gradient Descent(SGD)

원래는 전체를 하는 건데, n번의 데이터 즉 평균적인 것에 대해서 loss를 업데이트 해주어야 하는 것이다.
SGD는 일부, 즉 mini-batch 단위로 검토를 한 후 일단 발을 내딛어보는 거라고 할 수 있다.
SGD는 전체 학습데이터에서 하나씩 랜덤으로 뽑아 학습을 진행한다.
Problems with SGD
이러한 SGD방법에서 문제가 있다.

1. 학습 속도가 느리다.
먼저 2차원에서 loss가 한 방향으로는 빠르게, 다른 한 방향으로는 천천히 변화한다고 생각해보자. 그럼 이렇게 loss function 그래프가 그려진다. 그러면 학습이 진행될 때 경사가 완만한 가로축 방향으로는 작게, 경사가 급한 세로축 방향으로는 크게 움직이기 때문에 지그재그로 움직이게 되는 것을 볼 수 있다.
이 문제는 고차원으로 갈수록 더 많이 발생하고, Neural networks는 parameter의 개수가 매우 많기 때문에 이 모든 parameter들이 위의 그림에서와 같이 서로 다른 방향으로 움직이며 얽히게 되면 학습 속도가 매우 느려질 수밖에 없.

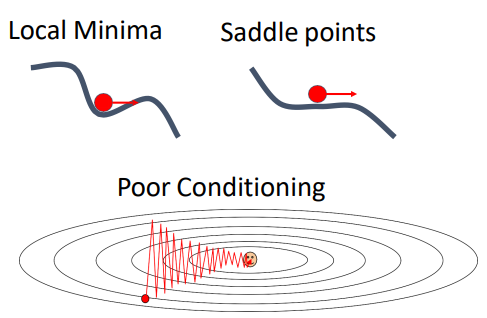
2. local minimum과 saddle point에 빠질 수 있다. (gradient =0)
다음으로, 이러한 골짜기가 있는 loss function에서 SGD는 local minima와 saddle point에 빠질 수 있다는 치명적인 단점이 있다. Local minimum의 경우 기울기가 0이 되어버리기 때문에 찾았다고 착각하고 멈춰버리게 된다. Saddle point 근처에서도 gradient가 0에 가까워지는 상황이 발생하고, gradient가 매우 작은 값이라 정말 학습이 느리게 진행되는 문제가 발생할 수 있다. 고차원에서는 local minimum보다 saddle points가 더 자주 발생하게 된다. 왜냐하면 parameter가 1억개가 된다고 해보면, 현재 포인트에서 일부 방향은 손실이 증가하고 일부 방향은 손실이 감소하는 상황이 거의 모든 곳에서 발생할 것이니까.

3. mini-batch 단위로 계산하기 때문에 noise에 취약하다.
mini-batch를 사용하기 때문에 step마다 정확한 gradient를 담을 수 없다. 일부 data를 추출해서 학습을 진행하는 것이기 때문에, gradient를 측정할 때 noise가 있으면 SGD가 최소값에 도달하는데 더 오래 걸릴 수도 있다. 오른쪽 그림을 보시면 일부러 noise를 준 상황이다. 열심히 헤매고 있는 것을 볼 수 있다.
즉, 그래서 Gradient가 0일 때도 멈추지 않도록 하는 방법이 필요하다!
SGD + Momemtum

1. 관성을 사용해 gradient가 0일 때도 멈추지 않도록 한다.
즉, mini-batch의 gradeint 방향과 velocity를 함께 고려한다.
말 그대로 관성을 추가해서 local minimum나 saddle point에서 벗어날 수 있도록 하는 방법이다.
SGD는 위치값(현재 파라미터 값)에 그라디언트가 직접 합쳐진다면, 모멘텀 업데이트는 물리학적 관점에서 그라디언트가 오직 속도(velocity, 과거의 값)에만 직접적으로 영향을 주고, 그 속도가 위치값(position)에 영향을 주게 된다.
모멘텀 업데이트를 쓰면, (파라미터 벡터가 업데이트 되는) 속도의 방향은 그라디언트들이 많이 향하는 방향으로 축적된다. 기존 SGD에서 velocity term이 추가된 버전이라고 이해하면된다. Velocity term은 속도를 조절하는 역할을 맡아 이러한 관성 효과를 내게 된다.
오른쪽 코드를 보면 너무 빠르게 가지 않도록 일종의 마찰을 주는 것이다. 이를 통해 gradient vector 방향 그대로 가는 것이 아니라, velocity vector의 방향으로 나아가게 된다. 모멘텀을 추가함으로써 속도가 생기면 노이즈가 평균화된다는 것을 이용한 방법이다.
왜 관성을 추가했느냐? 만약에 매 스텝마다 gradient가 동일한 부호를 가지면 v의 절댓값은 계속 증가할 수밖에 없다. (같은 방향으로 계속 이동하고 있으니까.) V가 증가함에 따라 x의 변화폭이 커지고, 이는 같은 방향으로 이동할수록 더 많이 이동하도록 가속화한다는 말과 같다.
이러한 특징 덕분에 위에서 SGD의 한계점으로 언급되었던 local minimum나 saddle point에서 gradient가 0에 수렴하는 값을 가진다 하더라도 이전 step들에서 축적되어온 v값이 더해지며 멈추지 않고 그 지점을 통과할 수 있게 되는 것이다.(local minimium에서 gradient가 0이 되더라도, 그 지점에서 속도를 여전히 갖고 있을테니까)
Saddle point에서도 그 주변 기울기는 매우 작을 수 있으나, 그 지점까지 가는데 발생한 속도 벡터가 존재하면 그 지점을 계속해서 통과해서 아래로 나아갈 수 있게 되는 것이다.
Nesterov Momentum

2. 관성 방향으로 움직인 자리에서 gradient로 next step을 계산한다.
-> 실제로 움직이는 것은 아니다. 관성 방향으로 이동한 자리에서 예측 후, 원래 지점에서 계산한다.
그 다음 등장한 Nesterov Momentum은 momentum과 비슷하지만 살짝 다르다. 그림은 붉은색 원에서 모멘텀에 의해 연두색 화살표의 끝점으로 이동할 상황이다.
Nesterov 모멘텀은 현재 위치에서 그라디언트를 계산하는 것이 아니라 이 "예견된" 위치(화살표 끝점)에서 그라디언트를 계산하는 것이다.
이렇게 되면 gradient를 계산하는 지점과 실제로 이동하는 지점이 다르다. 이는 이전 velocity와 현재 velocity의 차이를 반영하여 급격한 슈팅을 방지한다는 측면에서 효과가 있고, 더 빠른 학습을 가능하게 한다고 한다.
AdaGrad

3. 각각의 매개변수에 맞게 맞춤형으로 매개변수를 갱신한다.
-> 기울기 제곱에 반비례하도록 learning rate를 조정한다.
지금까지 논의된 방법들은 모두 모든 파라미터에 똑같은 learning rate를 적용했다. 다음은 업데이트 횟수에 따라 learning rate를 조절하는 방식에 대해서 알아보겠다.
Learning rate를 조절하는 건 굉장히 계산이 많은 작업이라 데이터에 맞춰서, 적응적으로 학습 속도를 정하는 방법을 찾고자 많이 노력했다. AdaGrad도 데이터에 맞게 학습 속도를 조정하는 방법 중 하나이다.
AdaGrad는 각각의 매개변수에 맞게 맞춤형으로 매개변수를 갱신하는 알고리즘입니다. 적응적으로 학습률을 조정하는 것이다. 기울기 제곱에 반비례하도록 학습률을 조정하는데, 이는 기울기가 가파를수록 조금만 이동하고, 완만할 수록 더 이동하게 함으로써 변동을 줄이는 효과가 있다. 무엇보다 가중치마다 다른 학습률을 적용한다는 점에서 더욱 정교한 최적화가 가능해집니다.
기울기가 가파를수록(클수록) 조금씩 이동하도록
-> 각 자중치마다 다른 learning rate를 적용해 변동을 줄이는 효과
그런데 여기서도 문제가 발생한다. 아무리 좋은 값이라고 하더라도 결국 학습이 진행될수록 이 h는 축적될 수밖에 없다. 이 분모값이 커질수록 이와 반비례하여 이동하는 보폭이 step을 진행할수록 작아지게 된다. 그만큼 처음에 올바른 지점으로 접근할 때 속도가 빨랐다가 점차적으로 속도가 느려진다.
이렇게 되면 결국 기울기가 0인 부근에서 학습이 급격하게 느려져서 local minima와 saddle point에서 업데이트가 되지 않는 문제가 발생할 위험이 커진다.이렇기 때문에 convex한 경우에는 매우 좋지만, convex하지 않을 때는 도중에 멈출 수도 있다.
RMSProp

4. AdaGrad처럼 보폭을 갈수록 줄이되, 이전 기울기의 맥락을 고려한다.
-> decay rate를 사용해 이전 스텝의 기울기를 더 크게 반영하여 h값이 단순 누적되는 것을 방지한다.
이 문제를 해결하고자 RMSProp이 등장했다. AdaGrad의 gradient 제곱항을 그대로 사용하는데, 핵심은 보폭을 갈수록 줄이되 이전 기울기 변화의 맥락을 살피자는 것이다. Adagrad식의 h와 squared gradient에 각각 p, (1−p)의 decay rate가 붙는다.
보통 p=0.9 정도로 설정되는데, 이렇게 되면 이전 스텝의 기울기를 더 크게 반영하여 h 값이 단순 누적되는 것을 방지할 수 있습니다. 이 과정을 "지수 가중 이동 평균"이라고 한다. 쉽게 말해서 무작정 보폭을 줄이지 않도록 옆에서 말리는 역할이라고 이해하셔도 좋을 것 같다. 이는 adagrade와 매우 비슷하기 때문에 step의 속도를 가속/감속할 수 있지만, momentum과 비슷하게 앞에서 온 값을 적용시켜주기에 속도가 줄어드는 문제를 해결할 수 있다.
h가 무한히 커지지 않으면서 p가 작을수록 가장 최신의 기울기를 더 크게 반영해 무조건적인 slow down을 방지한다.


Adam

먼저 아직 완벽한 아담은 아니고 아담과 가장 비슷한 형태의 optimizer이다.
먼저 Second_moment를 0으로 초기화한 상태이다. 이제 한 번의 업데이트를 진행하고 나면, beta2(second_moment의 decay rate)가 0.9 또는 0.99와 같이 1에 매우 가깝게 된다. 또 한 번의 업데이트 후에도 second_moment는 여전히 0에 가깝다. 이제 여기에서 learning rate를 second_moment로 나누면 아주 작은 수로 나누게 되는 것이다. 그럼 learning rate가 엄청나게 커질 수 있고, 이렇게 큰 learning rate는 잘못된 방향으로 학습하게 될 가능성이 크다.

그래서 bias correction이 추가된 것이 바로 adam이다. 첫 timestep이 매우 매우 컸던 문제를 해결하기 위해서 bias correction 과정을 통해 first, second moment 값을 0으로 시작할 수 있도록 만들어준다고 이해하면 된다.

사실 이렇게만 보면 이게 어떤 과정인지 잘 이해가 안 가실 것 같아서 수식으로도 준비했다.
이 식을 보면 우리는 이러한 사실들을 알 수 있다. 첫째로, Mt의 식에서 빨간색 박스 속 gt를 보니 이것은 gradient를 중심으로 하는 모멘텀 계열이라는 것을 알 수 있다. 둘째로, 그 아래 파란색 박스 속 gt^2를 보니 vt는 gradient 제곱에 반비례하는 ada, rmsprop 계열이라는 것을 알 수 있다. 마지막으로 mt와 vt모두 rmsprop 슬라이드에서 봤던 decay rate가 포함된 가중평균식과 비슷하다는 것을 알 수 있다.
그럼 여기서 저 1차 2차 moment는 Moment란 ‘적률’이라는 개념이다. 기본적으로 통계학에서 n차 적률이라고 하면 Xn의 기댓값을 의미한다. 우리가 알고 있는 모평균은 원래 X의 1차 적률이었고, 분산을 구할 때 자주 등장하는 E(X^2) 이것은 X의 2차 적률이라고 불린다. 우리는 표본평균과 표본제곱평균을 통해 모수에 해당하는 이 1차 적률과 2차 적률을 추정하는 것이다. 즉, Gradient의 1차 2차 moment에 대한 추정치는, 각각의 모수인 E(Gradient)와 E(Gradient2)를 추정하는 값을 가리키는 말이다.

'Lecture > 딥러닝' 카테고리의 다른 글
| [딥러닝] Evaluation Metrics & Training Neural Networks, Part I (0) | 2023.05.18 |
|---|---|
| [딥러닝] Convolutional Neural Network(CNN) (0) | 2023.05.18 |
| [딥러닝] Neural Network (0) | 2023.05.18 |
| [딥러닝] Supervised Learning, 지도학습 (2) | 2023.05.15 |
| [딥러닝] Intro (0) | 2023.04.06 |




댓글