Supervised Learning
- Linear Regression
- k Nearest Neighbors
- Linear Classifier
- Cost Function
Linear Regression (= 선형회귀)

- 회귀, 들어오는 input값을 기준으로 y값을 예측하는 모델이다.
- 한 개 이상의 독립 변수()와 종속 변수() 사이의 선형 상관 관계를 정략적으로 추정하는 회귀 분석 방법
- y = ax + b


- 위의 표에 있는 Data를 통해 학습시키는 것을 training이라고 한다.
- 그리고 이를 토대로 Regression이 결과를 예측한다.
- 데이터에 맞는 선을 찾는 것이 목표라고 할 수 있다.
- 즉, W,b를 구해야 하는 것이다.
이 때 사용하는 것이 Cost Function이다.
Cost : How fit the line to out (training) data
함수를 만들 때 가정을 하고 만들기 때문에 H인 것이다.

H와 y의 차이(얼마나 정확한지 일듯) 제곱의 합을 평균낸 것인데, Mean Squared Error(MSE)라고 한다.
그리고 이것의 평균이 cost이다.
Goal : Minimize cost

수학 기준으로 대상이 되는 함수를 최소화 한다는 의미.
즉 w,b의 계수에 의해 결정되는 것이며, 바꿀 수 있는 계수들을 minimize 한다는 것
Regression Metrics(참고)
Regression Metrics는 Regression을 얼마나 잘했는지 확인할 때 사용하는 평가지표.
1. RMSE (Root Mean Squared Error)

- 여기서 mean은 차이의 제곱이고, 이 식에서는 루트를 한다.
- i = 1~n까지, 즉 각각의 데이터 포인트를 구한다.
- ŷ은 Prediction의 결과
2. MAPE (Mean Absolute Percentage Error)

~예측한 값과 값 사이의 상관관계
3. MSE (Mean Squared Error)

4. MAE (Mean Absolute Error)

자, 그런데 중요한 것은 cost를 어떻게 최적화 할 것인가? 이다.
즉, Cost Function을 어떻게 최적화, parameter를 찾을 것인가?

단순하게 점들이 있을 때 그림을 그려보면, 원점을 지나는 어떤 함수를 찾을 수 있다.
여기서 차이의 제곱의 평균을 구하면 어떤 값의 평균이 나오고, 이것은 W의 2차식이 된다.
이것들을 다 모아서 나타내면 된다.
임의의 좌표라고 생각했을때 2차함수가 있을것이고, 최솟값이 존재한다.
즉, 이것을 통해서 cost함수의 최솟값을 구할 수 있다.
단순하게 미분해서 0이 되는 곳이 최솟값을 가질 수 있다.
그런데 문제는 2차식으로 표현되는 함수가 글로벌해서 찾을수가 없게 될 것이다.
그 때 쓰는 방법이 Gradient Descent 알고리즘이다.

우리말로는 경사하강으로 기울기를 따라 내려간다는 뜻이다.
초기값을 찍고 우리가 원하는 방향으로 진행되도록 방향을 찾는 것이다.
여기서 기울기는 W가 변할 때의 cost함수이다.


미분했을 때 어떻게 변하는가?
기울기의 반대방향으로 업데이트하면서 다음 W의 미분값을 빼준 것을 그 다음 값에 넣자.
그 방향으로 내려가면 값을 업데이트해서 잘보면 기울기가 0인 곳이 나올 수 있다.(2차함수, 아래로 볼록)
이렇게 러닝메이트를 어떻게 조절하고 선택할 것인가를 결정해야한다.
:=
다음 W에 이 값을 넣겠다는 의미
Logistic Regression
우리가 어떻게 좌표공간에 놓아야 최적화할 수 있을까? 라는 문제가 생긴다.

실제로는 연속적인 세계지만, 2가지의 이분법적인 사고로 표현을 한다.
어떤식으로 데이터를 만들것인가 ?
어떻게 사진을 찍는가에 대한 각도나 복잡한 문제에 대해서 어떻게 풀 것인가?
두 점사이의 거리의 최솟값을 찾는 식으로 비교를 해야한다.
Distance Metric to compare images


절대값의 합을 구하는 것이 L1, 픽셀값의 제곱의 합을 구하면 L2
k Nearest Neighbors
Overfitting intuition
얼마나 다른 함수를 쓰느냐에 따라 함수가 달라진다.
그래서 어떤 데이터가 들어오더라도 너무 단순화하는 것보다는 함수의 복잡성을 유지하되 잘 예측하도록하는 것이다.

복잡한 함수를 쓸수록 training data error가 줄어든다.
그래서 목적은 최대한 미래를 잘 예측하면서, 최대한 복잡성을 잘 유지하도록 !
Hyperparameters
- 함수의 차수, 처음부터 가정하고 가는 것
- 학습되는 계수들을 파parameter라고 하는 것이고 Hyperparameter 상위개념
k를 어케 정함?
이것은 validation 이랑 test를 하는 것이다.

hyperparamer 자체도 데이터로 결정하니까 또 다른 데이터로 깨끗하게 실험을 하기위해서 다른 데이터인 test로 하면, 최적화와 상관없이 우리의 정확한 성능을 알 수 있는 것이다.
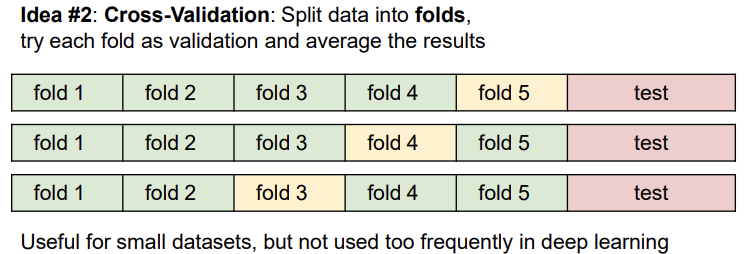
훈련셋을 여러개로 나누고 번갈아가면서 검증셋을 지정해준다.
데이터셋에서 먼저 테스트셋을 분리한 뒤, 나머지 데이터셋을 fold라는 단위로 나눈다. 그 후 fold들 중에 검증셋을 선택하는 과정을 반복한다.
위의 예제는 5개의 폴드 교차 검증이다. 먼저 fold 1-4에서 학습시키고 fold5에서 검증한다. 그 후 fold1-3,5에서 학습시키고 fold4에서 검증한다. 이처럼 반복하는 것을 볼 수 있다.
이를 통해 최적의 하이퍼파라미터를 얻을 수 있지만, 계산량이 많기 때문에 보통 작은 데이터셋일 경우 주로 사용하고, 딥러닝에서는 잘 사용하지는 않는다
Linear Classifier
- Neaural Network를 구성하는 가장 기본적인 요소
- Parametric model의 가장 단순한 예제
Linear Classifier의 종류는 다음과 같이 3가지이다.

1. Algebraic Viewpoint

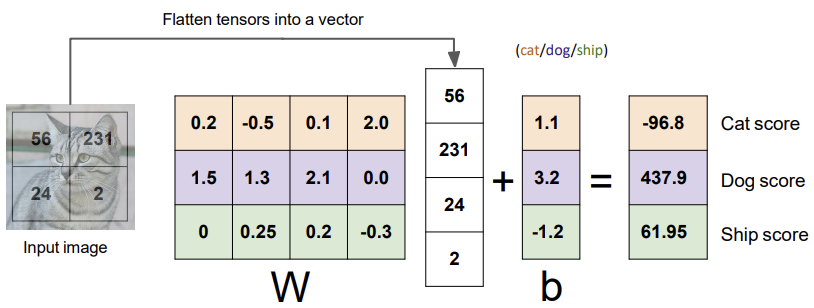
값으로 들어오는 것이 숫자인데, 이 픽셀의 값을 입력이라고 하자.
f(x,W) = Wx + b
- x : 입력 이미지
- W : 파라미터(가중치,weight), 세타(theta)라고도 한다.
- b : 바이어스(bias), 입력과 직접 연결되지 않고 대신 데이터와 무관하게 특정 클래스에 우선권을 부여
2. Visual Veiwpoint
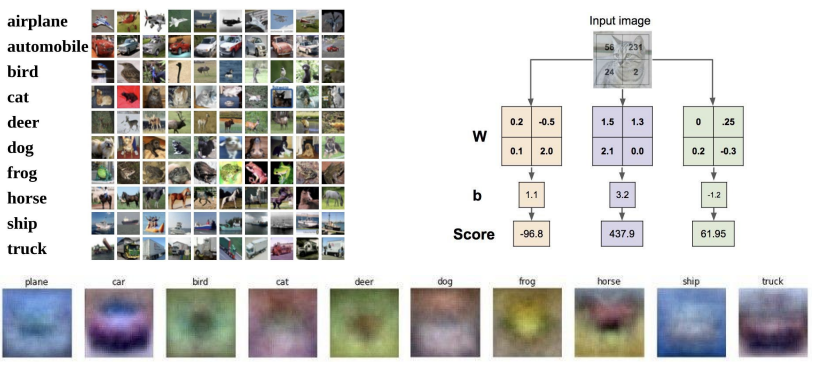
W들의 행을 이미지화함으로써 어떤 과정을 거치는지 알 수 있다. 즉, 입력이미지를 flatten 안시키고 그대로 사용하고 W도 같은 차원으로 만든후 각각을 곱해서 bias를 더한값을 스코어로 출력.
문제는 말의 머리가 2개라는 것 !
한 클래스 내에 다양한 특징들이 존재할 수 있지만, 모든 것들을 평균화시키기 때문에 클래스 당 하나의 템플릿밖에 허용하지 않으므로 이 방법이 최선이다.
3. Geometric Viewpoint

이미지를 고차원 공간의 한 점으로 보는 것이다. 각 이미지를 고차원 공간의 한 점이라고 생각했을 때 Linear classifier는 각 클래스를 구분시켜 주는 선형 결정 경계를 그어주는 역할을 한다. 하지만 Linear classifier로 분류하기 힘든 케이스가 많다.

다른 사분면에 있거나, 분포가 동그라미거나 이런것들을 해결하기 위해서 나중에 비선형 함수들을 더하게 된다.
Loss Function & Optimization
Loss Function
학습을 통해 얻은 데이터의 추정치가 실제 데이터와 얼마나 차이나는지 평가하는 지표로 쓰인다. 좋은 가중치 값을 찾기 위한 함수로 loss 값이 낮을 수록 좋은 분류기라고 한다. 비용 함수(cost function), 목적 함수(object function)라고 부르기도 한다. 정답이라고 하는 레이블, 각각의 사진들을 의미한다.

SVM loss
: 차이를 극대화 한다. 힌지로스
즉, 차이를 극대화 한다는 관점이다.

정답 클래스의 스코어값이 다른 스코어 값+1보다 크면 0, 그렇지 않으면 Sj-Syi+1 값을 갖는다.
- 정답스코어와 정답이 아닌 스코어간의 마진에 신경씀
- 일정 선(margins)을 넘기만 하면 더이상 성능개선에 신경쓰지 않는다.
Softmax Classifier

- 확률을 구해서 -log(정답클래스)
- 정답스코어가 충분히 높고, 다른 클래스스코어가 충분히 낮은 상태에서도 최대한 정답 클래스에 확률을 몰아넣으려고 할 것이고, 정답클래스는 무한대로, 그외의 클래스는 음의 무한대로 보내려할 것이다.
- 성능을 더 높이려할 것이다.
- 최종적인 목표는 정답 class에 대한 log 확률을 최대화 하는 것이다.
Cost Function

'Lecture > 딥러닝' 카테고리의 다른 글
| [딥러닝] Evaluation Metrics & Training Neural Networks, Part I (0) | 2023.05.18 |
|---|---|
| [딥러닝] Convolutional Neural Network(CNN) (0) | 2023.05.18 |
| [딥러닝] Backpropagation, Optimization (0) | 2023.05.18 |
| [딥러닝] Neural Network (0) | 2023.05.18 |
| [딥러닝] Intro (0) | 2023.04.06 |




댓글