Recap: 들어온 사진들이 fixel(x값), 에 곱해서 확률값을 해서 softmax값의 확률이 1이되도록 w를 찾앗었다.
말에대한 여러 사진이 있다. 말을 선택해야 하는데. 결과적으로 보면 말의 머리가 양쪽에 그려진 말이 생성되었다 다른 말을 했었다.

데이터가 양쪽에 잇는데 선형 분류기의 한계가 나타난다.
왼쪽은 Linear한 경계를 그릴 방법이 없다. 그런데 오른쪽 처럼 적절하게 특징 변환을 하면, 복잡하던 데이터가 변환 후에 선형으로 분리가 가능하게 바뀐다. 그래서 Linear classifier로 완벽하게 분리할 수 있다.
Biological Neuron

신경에서도 어느 신호 이상이 들어오면 확 변경된다. 즉 어느 이상 값이 들어오면 갑자기 증가하는 것을 보여준다.
우리도 어떤 값들이 들어오면 activation function에 의해서 변하게 된다.
기본적으로 신경망 같은 이러한 구조는 특징이 input으로 들어가 각각의 Weight들이 곱해지는 것이다.
Activation functions

가끔 미분가능하지 않아서 문제가 되는 경우가 있다. 그래서 Leaky ReLU를 사용한다.
Neural networks (fully connected network)

- 들어오는 모든 데이터를 모두 Weight들을 곱해서 다음으로 넘겨주는 것이다. 그래서 fully이다.
- 가장 기본이 되는 것은 2-layer이다.
- layer가 2가지 있어야 neural network라고 한다.
- 다른 말로 multi-layer perceptrons(MLP)라고 부르기도 한다.
왜 max(0, W1x)라는 식이 쓰였을까?
바로 non-linearity, 즉 비선형 식이 쓰여야 하기 때문이다.
non-linearity 식이 중간에 껴들어가지 않는다면, 아무리 많은 레이어들을 합쳐봤자 결국 하나의 레이어와 같은 결과를 내기 때문이다.
3 layers

f=W3*max(0 , W2*max(0, W1x))
미리 만들어뒀던 2-layer를 그냥 따와서, non-linear 한 함수에 집어넣고, 다시 다른 레이어로 덮어 씌우면 된다.
마찬가지로, 4-layer은? 5-layer은 위의 f값에서 레이어를 하나씩, 하나씩 더 씌우면 된다.
Neural Networks

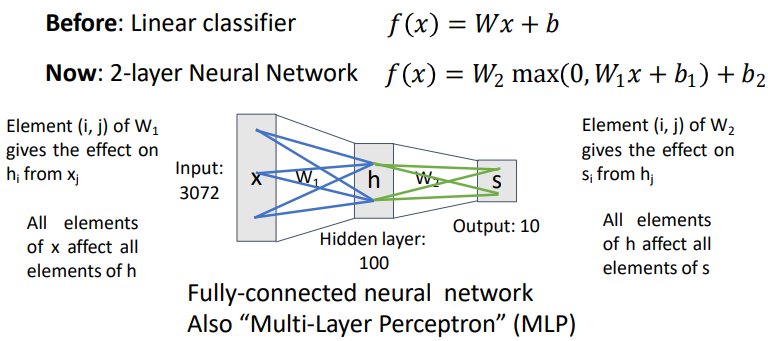
여기서는 hidden layer의 갯수만큼 layer가 생긴다.
그렇게 만든 템플릿을 조합해서 다시 만들어야 한다.
최종 스코어마다 생기는 것이다.
결과적으로 조합해서 여러가지의 ouput값을 조합해서 이것을 하나에다가 곱하는 것이다.
즉, 모든 input이 output에 영향을 주는 것이다.
Q. why is max operator important?

max를 씌우지 않으면 w1과 w2를 한 것이다. 결국 원래랑 같다
discriminative, 즉 모델의 복잡도 혹은 잠재능력이 늘어나지 않는다.
그래서 중간에 activation function을 곱해야 한다.
Space Warping with ReLU
왜 이것이 작동하는가?
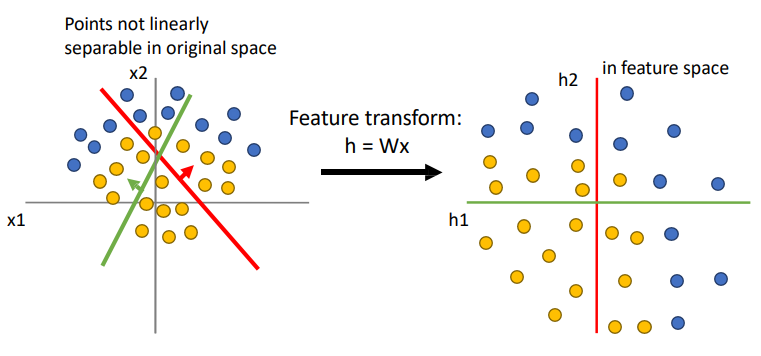
왼쪽의 점들을 새로운 축으로 보면, 하나의 축으로도 data를 잘 표현할 수 있다.
이것은 선형변환 할 수 있다는 것인데, 즉 보이는 좌표축들이 새롭게 변하는 것이다.
h라는 좌표공간에서 보았을 때, h1,h2는 새롭게 정의된 좌표 공간이다.
여기서 선형적으로 변환이 불가능한데, ReLU를 이욯해서 변형해보자.
ReLu는 0 이하의 값들에 대해 0의 값을 반환하므로, 데이터를 1사분면으로 변환시킨다. 따라서 아래 그림과 같이 Linearly separable한 특성공간이 만들어진다.
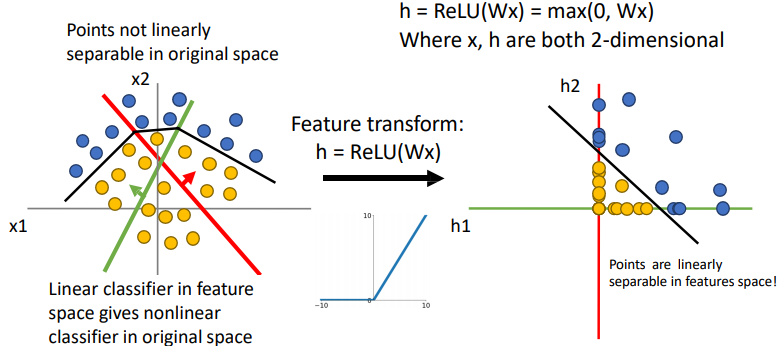
그럼 결과적으로 데이터가 변화한다.
이렇게 변형했을 떄 선형분류기로 선을 그어버리면, 쉽게 데이터들이 분류가 되게 바뀌게 되는 것이다.
즉, 선형변환과 활성함수를 모두 적용한 feature transformation을 통해 non-linear한 decision boundary를 생성할 수 있다. 이는 곧 신경망을 통해 non-linear function을 근사할 수 있다는 말이고, 이러한 점이 인공신경망을 매우 강력하게 해준다.
Regularization
학습하고자 하는 parameter에 제약을 걸어버리는 것이다.
이것이 없으면 학습이 잘 되지 않는다.

이 경우에 loss가 0이면 w가 유니크할까? -> 그렇지 않다!
이걸 막는 것이 regulation이다.

Loss 뒤에 weight에 대한 패널티를 부여하는 것이다.
왜 제약을 가하면, 모델의 복잡성이 높으면 overfitting(과적합)될 수 있다. 즉, 과적합을 해결하는 것이다.
가중치(w)에 제약을 건다. Regulaion을 사용하면 w값이 작아지면서 선형함수화 되는 것을 확인할 수 있다. 즉, 복잡한 함수가 아닌 간단한 함수가 되고, 이것은 모델의 크기를 줄이는 것과 같은 효과이다.
1) L1 Regulation(규제화)
L1 Regulation은 대부분의 가중치(W)를 0으로 만든다. 이를 통해 모델을 Sparse하게 만든다.
이것은 반면 어떤 특성들이 모델에 영향을 주고 있는지 정확히 판단해준다.
2) L2 Regulation (규제화)
L2 Regulation은 L1 Regulation과 다르게 가중치(W)들의 제곱을 최소화하므로, 가중치(W)의 값이 완전히 0이 되기보다 0에 가까워지는 경향을 가지고 있다.

w1과 w2는 1이라는 다 같은 결과를 가진다.
L2관점에서는 고른 분포가 더 적게된다.
L1에서는 계산을 하면 w1이 더 좋다. 즉, 전체적으로 합은 같지만 하나가 높은게 좋다.
즉, L1은 나머지를 0으로 만들어 버리는 것이다.
L2는 전체적으로 값은 비슷한데 작게 만드는 것이다.
'Lecture > 딥러닝' 카테고리의 다른 글
| [딥러닝] Evaluation Metrics & Training Neural Networks, Part I (0) | 2023.05.18 |
|---|---|
| [딥러닝] Convolutional Neural Network(CNN) (0) | 2023.05.18 |
| [딥러닝] Backpropagation, Optimization (0) | 2023.05.18 |
| [딥러닝] Supervised Learning, 지도학습 (2) | 2023.05.15 |
| [딥러닝] Intro (0) | 2023.04.06 |




댓글