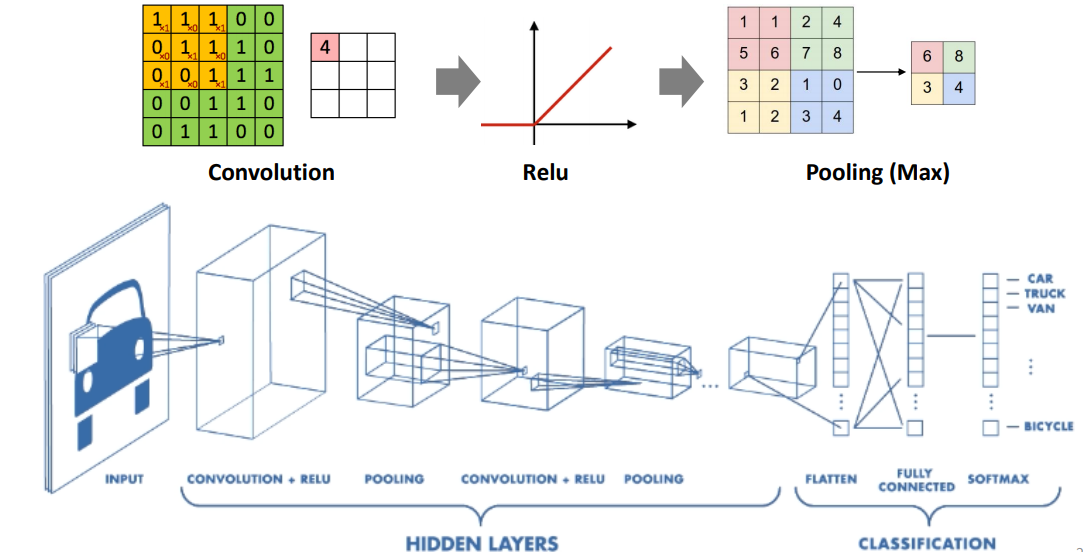
convolution이란 합성곱을 의미한다. 앞으로 CNN에서 Convolutional layer를 입력데이터가 지나면서, 이 합성곱이라는 과정을 거치게함수를 쭉 더해나가서 변형하는 형태로 쓰이게 되는 것이다.
그리고 0보다 작은건 0이고, 0보다 크면 그대로 쓰는 ReLU를 사용한다.
MAX pooling은 모아서 하나로 묶는 것이다.
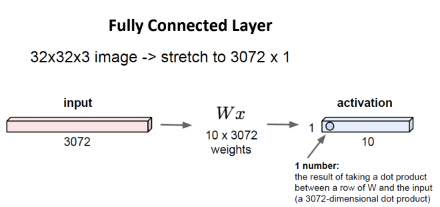
저번 강좌에서 배웠던 Fully Connected Layer을 다시 불러와 보자.
32*32*3의 이미지가 있으면, 그것을 3072*1의 크기로 변환시킨 것을 input값으로 했었다.
그리고, Wx값들은 (클래스 개수인) 10 * 3072로 만들어 둔 뒤에,
input과 Weight를 곱하여 10개의 output 값들을 만들어 내는 layer가 바로 Fully connected layer였다.
Convolution Layer
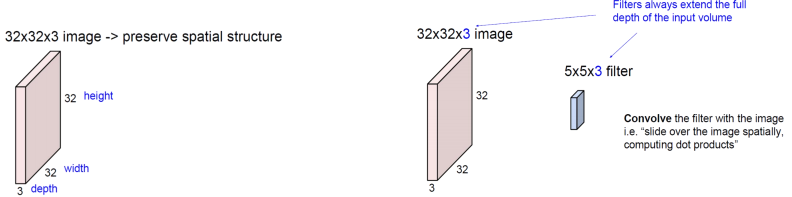
Convolution Layer은 Fully connected layer와 어떤 점이 다를까?
일단, Convolution layer에서의 input값은 fully-connected layer와는 다르게 원형을 보존한 상태로 둔다.
그리고, 우리의 weight값은 위의 자그마한 filter가 될 것입니다. (예에서는, 5*5*3의 크기)
가로와 세로의 크기는 input의 크기보다 크지만 않으면 되지만, 이 filter의 깊이는 무조건 input값과 같아야 한다. (여기서는 3)
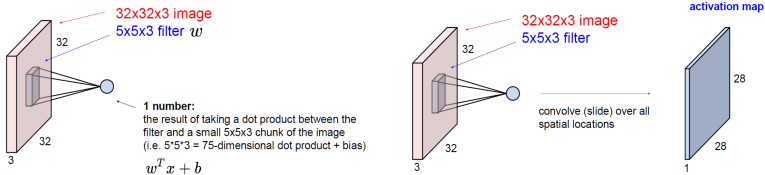
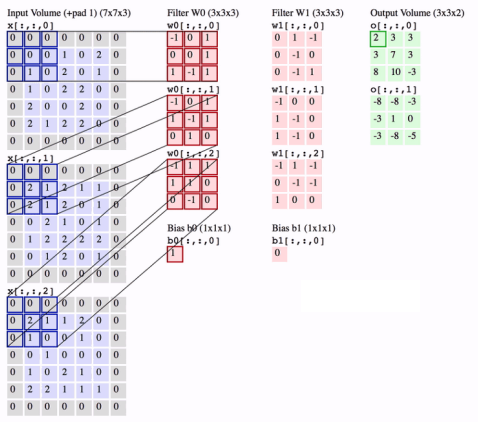
그리고, 이렇게 마련된 filter를, 왼쪽 위부터 모든 부분마다 점곱을 해준다. 즉, input 사진의 왼쪽 위 5*5*3 부분에 필터를 곱한 후에, 더하는 것이다. 그 후에, 한 칸 왼쪽으로 옮겨서 해주고.. 맨 위쪽 끝까지 갔다면 한 칸 아래로 내려서 다시 해주고.. 하는 것이다. 마치, filter를 image에다가 대고, 쭉 밀어준다는 느낌인 것이다.
그런 뒤에, 그런 뒤에, bias까지 더해준다.
그렇게 하나하나 다 곱해주다 보면, 다음과 같이 28*28*1 크기의 output이 나온다.
간단히 계산을 해본다면.. 왜 이런 결과가 나오는지도 계산이 가능하다.
그리고, 이 output값은 activation map(feature map)이라고 하는데, 이는 이 사진이 가지는 특징을 나타내어 주는 역할을 한다.
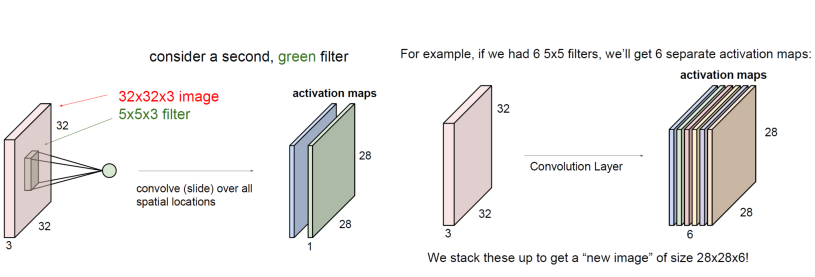
그런데, CNN을 사용할 때에는, filter를 하나만 사용하지는 않는다. 다양한 필터를 사용하여, 필터마다 다른 특징을 나타내게 만들 것이다.
저번 linear classification 시간에, 막 '자동차' 클래스의 weight는 빨간 자동차만을 나타내는 그림이 있었고, 말은 머리가 두 개 달려있었고.. 그랬는데, CNN은 그러한 단점을 없애기 위하여 다양한 필터를 사용한다. 그만큼 다양한 특징들을 추출해 내기 위함이다.
그리고, 필터를 두 개 사용했으니 activation map은 두 개가 나온다. 각각의 필터마다 점과 계산을 해 줄 테니 말이죠. 그러면, filter 6개를 사용한다면? 당연히 6개의 activation map이 나온다!
그리고, 이것을 쌓아본다면.. 우리는 28*28*6 크기의 output, 즉 activation map을 얻은 것이다.
Stride and Pad
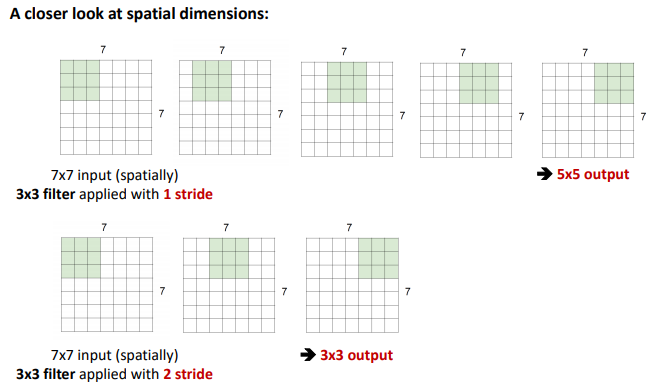
이렇게 쭉- 밀어나가며 점곱을 하게 될 것이다. 즉, 한 칸, 한 칸씩 오른쪽으로 옮겨주면서 계산하는 것이다.
그러면, output의 사이즈는 5*5의 사이즈가 될 것입니다. 한번 계산에 숫자 하나씩이라 하고 한번 밀어보면 된다.
2칸씩 밀면, output의 크기는.. 3*3의 크기가 된다.
이와 같이, 미는 정도를 stride라고 합니다.
가령, stride가 1이라면, 1칸씩 민다는 것이고.. stride가 2라면, 2칸씩 민다는 것이다.

이것은 산술적으로도 생각할 수 있다.
우리의 Output size는 (N-F) / stride + 1로 계산할 수 있다. (N=이미지 크기, F=필터 크기)
N=7이고 F=3일 때..
stride가 1이라면, output의 사이즈는 (7-3)/1 + 1 = 5,
stride가 2라면, output의 사이즈는 (7-3)/2 + 1 = 3이 되지만..
stride가 3이라면, (7-3)/3+1 = 2.33이 되므로, output의 사이즈가 성립하지 않다!
크기는 당연히 자연수여야 하니까..
Padding이란, 이미지의 가장자리 부분에 어떠한 숫자들을 채워 넣는 것을 의미한다.
그렇다면, 7*7 이미지에, stride가 1이고, padding을 1픽셀만 가장자리에 덮어씌워준다면, output의 크기는
아까 전에, output size는 (N-F)/stride + 1이라고 하였으므로, 이번엔 N=9 (엄밀히는 7+2), F=3, stride=1이니..
(9-3)/1 + 1 = 7이 된다. 즉, output은 7*7의 크기가 되는 것이다.
그리고, 일반적인 경우엔 convolutional layer은 stride는 1로 하고,
filter 크기가 F*F라면 padding은 (F-1)/2의 크기만큼 한다.
(N - F + 2*P) / stride +1

32*32*3 크기의 이미지에다가 계속해서 filter를 적용시켰을 때, 크기가 (깊이 빼고) 32*32에서 28*28, 24*24...로 빠르게 줄어드는 것을 확인할 수 있다. 그러면, CONV를 한 5번만 해도, 크기가 12*12 정도로 줄어들 터인데, 이는 사진의 부분적인 요소들을 보존하자는 취지를 생각하면.. 별로 좋지 못하다는 것을 쉽게 알 수 있다.
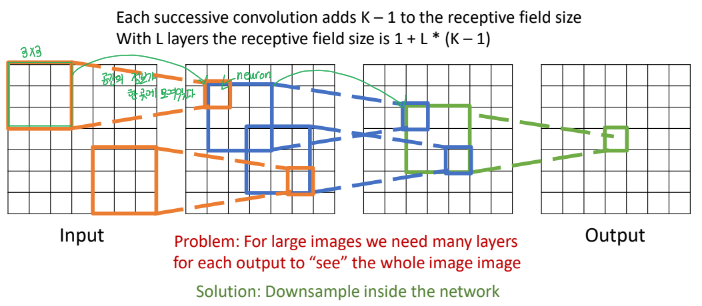
- output의 한 칸을 생성하기 위해서, 필터가 적용된 영역을 receptive field라고 한다.
- 연속적인 RF는 RF size에 K-1만큼 곱해준다.L-th layer의 RF size는 1+L*(K-1)이다.


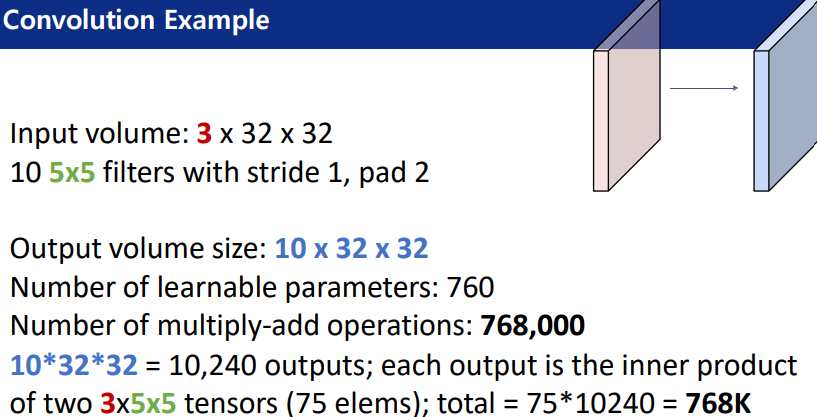
학습가능한 parameter의 수는, 10개의 5*5가 된다.
1*1 Convolution
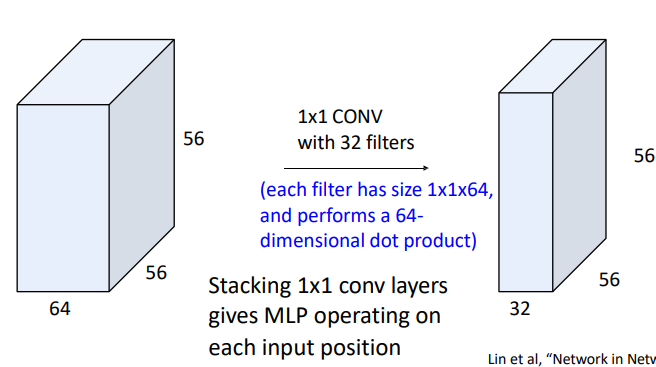
F=1, S=1, P=0 이 있었는데, filter의 크기가 1*1이어도 되나? 생각할 수도 있지만 그래도 된다.
padding이 없어도 크기가 그대로 유지되며, 다음 activation map도 아무런 탈 없이 나온다!
Other types of convolution

2D는 우리가 계속 보았던 것이다. 어떤 공간적인 correlation을 보는 것이다.
3D는 3차원적으로 공간적으로 뽑아야 한다. 모든 방향을 convolution을 하는 것이다. 동영상일 때는 시간 축을 하는 것이다. 이 때 사용되느 filter는 채널이라는 개수의 의미만큼 있는 것이다. 조그마한 박스를 C개 넣는 것이다.
Pooling Layer
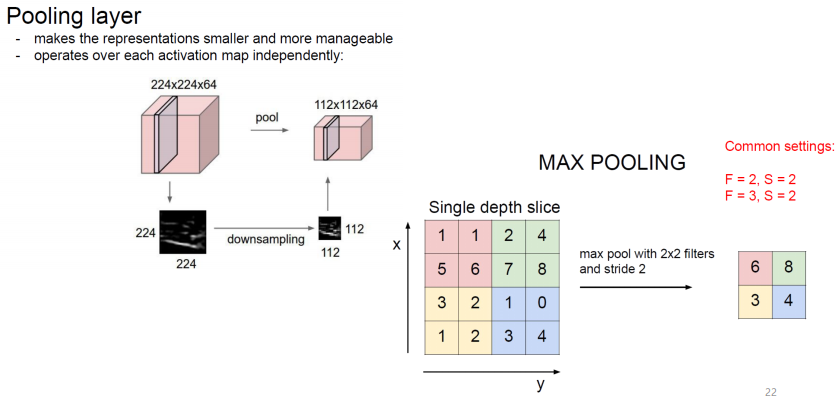
Pooling layer
- 폴링은 세로・가로 방향의 공간을 줄이는 연산이다.
'아니.. 아까 전에 이거 안 줄이려고 padding 한다며요? 근데 이번엔 또 왜 줄인대?'
왜 그러냐면.. 아까 전의 padding을 한 것은 크기 보존뿐만 아니라, 이미지의 부분적 특징을 살리기 위해서 한 것이다. 계속해서 convolution을 한다면, 가장자리 부분의 특징이 잘 살아나지 못한다.
하지만, 이번에 하는 pooling은, 이미지의 특정 부분을 잘라내는 것이 아니라, 사진 전체 부분을 유지한 상태로 픽셀만 줄이는 것입니다.
- stride와 다른 점은 학습해야할 매개변수가 없다는 점이다.
- pooling layer에서는 hyperparameter로 kernel size와 stride, pooling function만 신경쓰면 된다.
- 폴링 연산은 입력데이터의 채널 수 그대로 출력 데이터로 내보내기 때문에, 채널 수가 변하지 않는다.
게임의 해상도를 줄이는 것을 생각하면 이해하기 편하다.. 1920*1080 해상도로 게임하다가, 딱 그 반 크기로 게임을 한다면, 전체적인 화면은 똑같겠지만, 뭔가 조금 화질이 안 좋다는 느낌이 팍 든다. 뒤로 가면 갈수록 filter의 개수가 늘어나는 것이 일반적인데, 이런 식으로 늘여가다 보면 activation map의 깊이가 너무 깊어지게 되고, 위와 같이 224*224*64 같은 크기의 이미지가 되어 버린다.
그런데, 이렇게 된다면 계산하는 데에 너무 오랜 시간이 걸려서, 뭘 할 수도 없는 지경에 이르게 된다. 하지만, pooling을 해서 activation map의 크기를 반으로 팍 줄여준다면, 계산도 두배로 빨라지게 될 것이다.
이것도 게임을 생각하면 편합니다. 해상도를 줄이면, 그래픽카드와 CPU가 해야 하는 연산이 조금 더 줄어드므로.. 렉 걸리던 게임도 잘 돌아가게 되겠죠?
Max Pooling
위의 이미지에서는 2x2커널사이즈와 strade가 2인 2x2 Max pooling을 하는 내용이다. 각 영역에서 가장 큰 원소 하나를 꺼내는 것이다.
'Lecture > 딥러닝' 카테고리의 다른 글
| [딥러닝] Backpropagation Matrix Operation (0) | 2023.05.18 |
|---|---|
| [딥러닝] Evaluation Metrics & Training Neural Networks, Part I (0) | 2023.05.18 |
| [딥러닝] Backpropagation, Optimization (0) | 2023.05.18 |
| [딥러닝] Neural Network (0) | 2023.05.18 |
| [딥러닝] Supervised Learning, 지도학습 (2) | 2023.05.15 |




댓글